We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 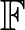\mathbb F be a finite field of odd order and 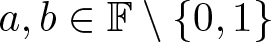a,b\in\mathbb F\setminus\{0,1\} be such that 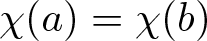\chi(a) = \chi(b) and 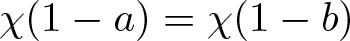\chi(1-a)=\chi(1-b), where χ is the extended quadratic character on 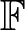\mathbb F. Let 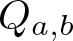Q_{a,b} be the quasigroup over 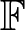\mathbb F defined by 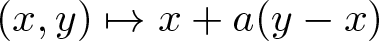(x,y)\mapsto x+a(y-x) if 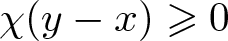\chi(y-x) \geqslant 0, and 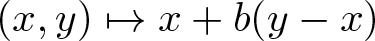(x,y)\mapsto x+b(y-x) if 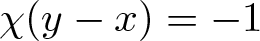\chi(y-x) = -1. We show that 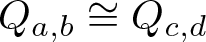Q_{a,b} \cong Q_{c,d} if and only if 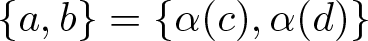\{a,b\}= \{\alpha(c),\alpha(d)\} for some 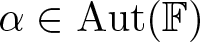\alpha\in \operatorname{Aut}(\mathbb F). We also characterize 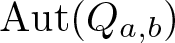\operatorname{Aut}(Q_{a,b}) and exhibit further properties, including establishing when 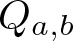Q_{a,b} is a Steiner quasigroup or is commutative, entropic, left or right distributive, flexible or semisymmetric. In proving our results, we also characterize the minimal subquasigroups of 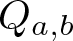Q_{a,b}.
Email your librarian or administrator to recommend adding this to your organisation's collection.
