Let 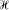 be a separable Hilbert space,
be a separable Hilbert space, 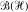 the algebra of all bounded operators on
the algebra of all bounded operators on 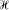 and Ai, Bi, ∊
and Ai, Bi, ∊ 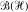 , i = 1,. . . , r. It is shown that if no nontrivial linear combination of the operators Ai, is compact, then there exist X, Y ∊
, i = 1,. . . , r. It is shown that if no nontrivial linear combination of the operators Ai, is compact, then there exist X, Y ∊ 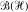 such that X Ai, Y = Bi, for all i. A related (but much milder) result is discussed in other algebras with the unique maximal ideal and an application to elementary operators is given.
such that X Ai, Y = Bi, for all i. A related (but much milder) result is discussed in other algebras with the unique maximal ideal and an application to elementary operators is given.