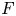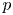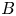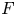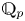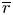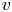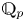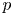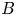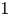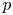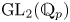1 results
On some mod p representations of quaternion algebra over ℚp
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2585-2655
- Print publication:
- November 2024
-
- Article
- Export citation