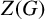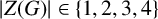1 results
FINITE GROUPS WITH ABNORMAL MINIMAL NONNILPOTENT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 261-270
- Print publication:
- April 2023
-
- Article
- Export citation