We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Bounds of exponential type are derived for the first-hitting time and occupation times of a real-valued random sequence which has a uniform negative drift whenever the sequence is above a fixed level. The only other assumption on the random sequence is that the increments satisfy a uniform exponential decay condition. The bounds provide a flexible technique for proving stability of processes frequently encountered in the control of queues.
Two applications are given. First, exponential-type bounds are derived for a GI/G/1 queue when the service distribution is exponential type. Secondly, geometric ergodicity is established for a certain Markov chain in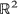 
which arises in the decentralized control of a multi-access, packet-switched broadcast channel.
