We use an interacting particle system on ℤ to model an epidemic. Each site of ℤ can be in either one of three states: empty, healthy or infected. An empty site x gets occupied by a healthy individual at a rate βn1(x) where n1(x) is the number of healthy nearest neighbors of x. A healthy individual at x gets infected at rate αn2(x) where n2(x) is the number of infected nearest neighbors of x. An infected individual dies at rate δ independently of everything else. We show that for all α, β and δ> 0 and all initial configurations, all the sites of a fixed finite set remain either all empty or all healthy after an almost surely finite time. Moreover, if the initial configuration has infinitely many healthy individuals then the process converges almost surely (in the sense described above) to the all healthy state. We also consider a model introduced by Durrett and Neuhauser where healthy individuals appear spontaneously at rate β > 0 and for which coexistence of 1's and 2's was proved in dimension 2 for some values of α and β. We prove that coexistence may occur in any dimension.

A spatial epidemic process where the individuals are located at positions in the Euclidean space R2 is considered. The infective individuals, with an infection period that is exponentially distributed with parameter µ, move in R2 according to a Brownian motion with a diffusion coefficient σ2. The susceptible individuals may also move. But we shall use the approximation that they remain unchanged in numbers and therefore assume that the averaged ‘density' of susceptibles per unit area is the same throughout space and time. The transition probability rate of infection of a susceptible in the infinitesimal element of area dy by an infective in dx is assumed to be a function h(x – y |) of the distance | x – y | between x and y. Then our process can be considered as a two-dimensional birth and death Brownian motion. 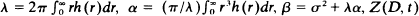Let be the number of infective individuals in the set 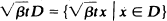D at time t and . The almost everywhere convergence of the random variables 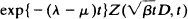to a limit random variable W(D) is established.