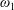1 results
Chains of P-points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 856-868
- Print publication:
- December 2019
-
- Article
- Export citation
-
It is proved that the Continuum Hypothesis implies that any sequence of rapid P-points of length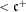
${<}\mathfrak{c}^{+}$ that is increasing with respect to the Rudin–Keisler ordering is bounded above by a rapid P-point. This is an improvement of a result from B. Kuzeljevic and D. Raghavan. It is also proved that Jensen’s diamond principle implies the existence of an unbounded strictly increasing sequence of P-points of length 
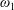$\unicode[STIX]{x1D714}_{1}$ in the Rudin–Keisler ordering. This shows that restricting to the class of rapid P-points is essential for the first result.
