It is known that all k-homogeneous orthogonally additive polynomials P over C(K) are of the form
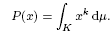
Thus, x ↦ xk factors all orthogonally additive polynomials through some linear form μ. We show that no such linearization is possible without homogeneity. However, we also show that every orthogonally additive holomorphic function of bounded type f over C(K) is of the form
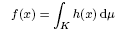
for some μ and holomorphic h : C (K) → L1(μ) of bounded type.