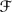Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (1)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

primary 37f75

Glasgow Mathematical Journal (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

GEOMETRIC INVARIANT THEORY FOR HOLOMORPHIC FOLIATIONS ON ℂℙ2 OF DEGREE 2
CLAUDIA R. ALCÁNTARA
Journal:

Glasgow Mathematical Journal / Volume 53 / Issue 1 / January 2011

Published online by Cambridge University Press:

22 December 2010, pp. 153-168

Print publication:

January 2011
- Article
- - You have access
- PDF
- Export citation
Let 2 be the space of the holomorphic foliations on ℂℙ2 of degree 2. In this paper we study the linear action PGL(3, ℂ) × 2 → 2 given by gX = DgX ^(g−1) in the sense of the Geometric Invariant Theory. We obtain a characterisation of unstable and stable foliations according to properties of singular points and existence of invariant lines. We also prove that if X is an unstable foliation of degree 2, then X is transversal with respect to a rational fibration. Finally we prove that the geometric quotient of non-degenerate foliations without invariant lines is the moduli space of polarised del Pezzo surfaces of degree 2.