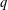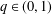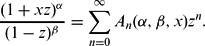D. Brannan's conjecture says that for 0 <α,β≤1, |x|=1, and n∈N one has |A2n−1(α,β,x)|≤|A2n−1(α,β,1)|, where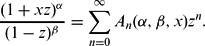 We prove this for the case α=β, and also prove a differentiated version of the Brannan conjecture. This has applications to estimates for Gegenbauer polynomials and also to coefficient estimates for univalent functions in the unit disk that are ‘starlike with respect to a boundary point’. The latter application has previously been conjectured by H. Silverman and E. Silvia. The proofs make use of various properties of the Gauss hypergeometric function.
We prove this for the case α=β, and also prove a differentiated version of the Brannan conjecture. This has applications to estimates for Gegenbauer polynomials and also to coefficient estimates for univalent functions in the unit disk that are ‘starlike with respect to a boundary point’. The latter application has previously been conjectured by H. Silverman and E. Silvia. The proofs make use of various properties of the Gauss hypergeometric function.
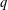 $q$-FUNCTION THEORY
$q$-FUNCTION THEORY