We prove that the infinitesimal variations of Hodge structure arising in a number of geometric situations are non-generic. In particular, we consider the case of generic hypersurfaces in complete smooth projective toric varieties, generic hypersurfaces in weighted projective spaces and generic complete intersections in projective space and show that, for sufficiently high degrees, the corresponding infinitesimal variations are non-generic.
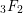 $_{3}F_{2}$
$_{3}F_{2}$