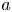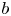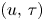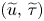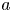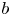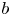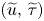This paper focuses on the vanishing limit problem for the three-dimensional incompressible Phan-Thien–Tanner (PTT) system, which is commonly used to describe the dynamic properties of polymeric fluids. Our purpose is to show the relation of the PTT system to the well-known Oldroyd-B system (with or without damping mechanism). The suitable a priori estimates and global existence of strong solutions are established for the PTT system with small initial data. Taking advantage of uniform energy and decay estimates for the PTT system with respect to time $t$ and coefficients $a$
and coefficients $a$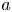 and $b$
and $b$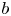 , then allows us to justify in particular the vanishing limit for all time. More precisely, we prove that the solution $(u,\,\tau )$
, then allows us to justify in particular the vanishing limit for all time. More precisely, we prove that the solution $(u,\,\tau )$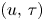 of PTT system with $0\leq b\leq Ca$
of PTT system with $0\leq b\leq Ca$ converges globally in time to some limit $(\widetilde {u},\,\widetilde {\tau })$
converges globally in time to some limit $(\widetilde {u},\,\widetilde {\tau })$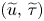 in a suitable Sobolev space when $a$
in a suitable Sobolev space when $a$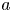 and $b$
and $b$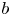 go to zero simultaneously (or, only $b$
go to zero simultaneously (or, only $b$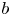 goes to zero). We may check that $(\widetilde {u},\,\widetilde {\tau })$
goes to zero). We may check that $(\widetilde {u},\,\widetilde {\tau })$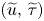 is indeed a global solution of the corresponding Oldroyd-B system. In addition, a rate of convergence involving explicit norm will be obtained. As a byproduct, similar results are also true for the local a priori estimates in large norm.
is indeed a global solution of the corresponding Oldroyd-B system. In addition, a rate of convergence involving explicit norm will be obtained. As a byproduct, similar results are also true for the local a priori estimates in large norm.