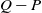We review criteria for comparing the efficiency of Markov chain Monte Carlo (MCMC) methods with respect to the asymptotic variance of estimates of expectations of functions of state, and show how such criteria can justify ways of combining improvements to MCMC methods. We say that a chain on a finite state space with transition matrix P efficiency-dominates one with transition matrix Q if for every function of state it has lower (or equal) asymptotic variance. We give elementary proofs of some previous results regarding efficiency dominance, leading to a self-contained demonstration that a reversible chain with transition matrix P efficiency-dominates a reversible chain with transition matrix Q if and only if none of the eigenvalues of $Q-P$ are negative. This allows us to conclude that modifying a reversible MCMC method to improve its efficiency will also improve the efficiency of a method that randomly chooses either this or some other reversible method, and to conclude that improving the efficiency of a reversible update for one component of state (as in Gibbs sampling) will improve the overall efficiency of a reversible method that combines this and other updates. It also explains how antithetic MCMC can be more efficient than independent and identically distributed sampling. We also establish conditions that can guarantee that a method is not efficiency-dominated by any other method.

We consider Markov processes, which describe, e.g. queueing network processes, in a random environment which influences the network by determining random breakdown of nodes, and the necessity of repair thereafter. Starting from an explicit steady-state distribution of product form available in the literature, we note that this steady-state distribution does not provide information about the correlation structure in time and space (over nodes). We study this correlation structure via one-step correlations for the queueing-environment process. Although formulas for absolute values of these correlations are complicated, the differences of correlations of related networks are simple and have a nice structure. We therefore compare two networks in a random environment having the same invariant distribution, and focus on the time behaviour of the processes when in such a network the environment changes or the rules for travelling are perturbed. Evaluating the comparison formulas we compare spectral gaps and asymptotic variances of related processes.

For exponential open and closed queueing networks, we investigate the internal dependence structure, compare the internal dependence for different networks, and discuss the relation of correlation formulae to the existence of spectral gaps and comparison of asymptotic variances. A central prerequisite for the derived theorems is stochastic monotonicity of the networks. The dependence structure of network processes is described by concordance order with respect to various classes of functions. Different networks with the same first-order characteristics are compared with respect to their second-order properties. If a network is perturbed by changing the routeing in a way which holds the routeing equilibrium fixed, the resulting perturbations of the network processes are evaluated.