In this paper we consider the growth rates of 3-dimensional hyperbolic Coxeter polyhedra with at least one dihedral angle of the form 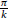 $\frac{\pi }{k}$ for an integer
$\frac{\pi }{k}$ for an integer 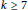 $k\ge 7$. Combining a classical result by Parry with a previous result of ours, we prove that the growth rates of 3-dimensional hyperbolic Coxeter groups are Perron numbers.
$k\ge 7$. Combining a classical result by Parry with a previous result of ours, we prove that the growth rates of 3-dimensional hyperbolic Coxeter groups are Perron numbers.