1 results
Stochastic asymptotic exponential stability of stochastic integral equations
-
- Journal:
- Journal of Applied Probability / Volume 9 / Issue 1 / March 1972
- Published online by Cambridge University Press:
- 14 July 2016, pp. 169-177
- Print publication:
- March 1972
-
- Article
- Export citation
-
The object of this paper is to study the stochastic asymptotic exponential stability of a stochastic integral equation of the form
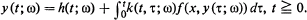
A random solution of the stochastic integral equation is considered to be a second order stochastic process satisfying the equation almost surely. The random solution, y(t, ω) is said to be. stochastically asymptotically exponentially stable if there exist some β > 0 and a γ > 0 such that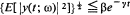
for t∈ R+.The results of the paper extend the results of Tsokos' generalization of the classical stability theorem of Poincaré-Lyapunov.
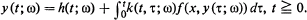
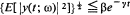for 