We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give an affirmative answer to Brendle's and Hrušák's question of whether the club principle together with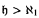 
is consistent. We work with a class of axiom A forcings with countable conditions such that 
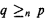is determined by finitely many elements in the conditions p and q and that all strengthenings of a condition are subsets, and replace many names by actual sets. There are two types of technique: one for tree-like forcings and one for forcings with creatures that are translated into trees. Both lead to new models of the club principle.
