Search

The assumption of linear costs of observation usually leads to optimal stopping boundaries which are straight lines. For non-linear costs of observation, the question arises of how the shape of cost functions influences the shape of optimal stopping boundaries. In Irle (1987), (1988) it was shown that, under suitable assumptions on c, for the problem of optimal stopping (Wt + x)+ - c(s + t), t ∊ [0,∞), the optimal stopping boundary h(t) can be enscribed between k1/c'(t) and k2/c'(t) for some constants k1, k2. In this paper we find the exact asymptotic expansion h(t) = 1/(4c'(t))(1 + o(1)).

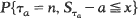A local limit theorem for is obtained, where τ a is the first time a random walk Sn with positive drift exceeds a. Applications to large-deviation probabilities and to the crossing of a non-linear boundary are given.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

An asymptotic expansion for the optimal stopping boundary in problems with non-linear costs of observation

Limit theorems for first-passage times in linear and non-linear renewal theory

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

An asymptotic expansion for the optimal stopping boundary in problems with non-linear costs of observation

Limit theorems for first-passage times in linear and non-linear renewal theory