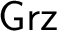1 results
NON-WELL-FOUNDED PROOFS FOR THE GRZEGORCZYK MODAL LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 22-50
- Print publication:
- March 2021
-
- Article
- Export citation