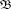Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (1)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

libera operator

Proceedings of the Edinburgh Mathematical Society (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Analytic functions with decreasing coefficients and Hardy and Bloch spaces
Miroslav Pavlović
Journal:

Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013

Published online by Cambridge University Press:

26 July 2012, pp. 623-635
- Article
- - You have access
- PDF
- Export citation
The following rather surprising result is noted.
(1) A function f(z) = ∑anzn such that an ↓ 0 (n → ∞) belongs to H1 if and only if ∑(an/(n + 1)) < ∞.
A more subtle analysis is needed to prove that assertion (2) remains true if H1 is replaced by the predual, 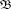1(⊂ H1), of the Bloch space. Assertion (1) extends the Hardy–Littlewood theorem, which says the following.
(2) f belongs to Hp (1 < p < ∞) if and only if ∑(n + 1)p−2anp < ∞.
A new proof of (2) is given and applications of (1) and (2) to the Libera transform of functions with positive coefficients are presented. The fact that the Libera operator does not map H1 to H1 is improved by proving that it does not map 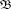1 into H1.