The longest stretch L(n) of consecutive heads in n independent and identically distributed coin tosses is seen from the prism of large deviations. We first establish precise asymptotics for the moment generating function of L(n) and then show that there are precisely two large deviation principles, one concerning the behavior of the distribution of L(n) near its nominal value log1∕p n and one away from it. We discuss applications to inference and to logarithmic asymptotics of functionals of L(n).

We take a fresh look at the classical problem of runs in a sequence of independent and identically distributed coin tosses and derive a general identity/recursion which can be used to compute (joint) distributions of functionals of run types. This generalizes and unifies already existing approaches. We give several examples, derive asymptotics, and pose some further questions.

General exact formulas are established to calculate the reliability of a consecutive-k-out-of-n: F system. The optimality of the system, under permutation of the components, is examined too.

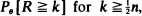Let Xl, · ··, Χ n be independent binary variables with parameters θl, · ··, θ n respectively, and let R denote the length of the longest run of 1's. This note concerns a new expression for and a rearrangement inequality. The inequality is applied to solve an optimal permutation problem for consecutive-k-out-of-n: F networks, and its implications on a recent conjecture of Derman et al. (1982) are discussed.