4 results
Some properties of two families of classes of life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-589
- Print publication:
- September 2002
-
- Article
- Export citation
A note on the ℒ-class of life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 11-19
- Print publication:
- March 2002
-
- Article
- Export citation
A useful ageing property based on the Laplace transform
-
- Journal:
- Journal of Applied Probability / Volume 20 / Issue 3 / September 1983
- Published online by Cambridge University Press:
- 14 July 2016, pp. 615-626
- Print publication:
- September 1983
-
- Article
- Export citation
On the limiting distribution of the failure time of fibrous materials
-
- Journal:
- Advances in Applied Probability / Volume 15 / Issue 2 / June 1983
- Published online by Cambridge University Press:
- 01 July 2016, pp. 331-348
- Print publication:
- June 1983
-
- Article
- Export citation

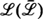 of life distributions for which
of life distributions for which 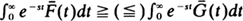 , where
, where 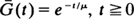 , and
, and 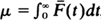 , is studied. We prove that this class is larger than the HNBUE (HNWUE) class (consisting of those life distributions for which
, is studied. We prove that this class is larger than the HNBUE (HNWUE) class (consisting of those life distributions for which 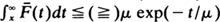 for
for 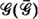 of discrete life distributions for which
of discrete life distributions for which 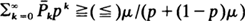 for 0 ≦
for 0 ≦ 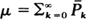 , is also studied.
, is also studied.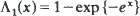 for
for 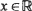 . Since fibrous materials which are both long and have many filaments prevail, the result is of importance in the materials science area since refined approximations to failure-time distributions can be achieved.
. Since fibrous materials which are both long and have many filaments prevail, the result is of importance in the materials science area since refined approximations to failure-time distributions can be achieved.