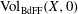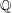2 results
On the volume of isolated singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 23 June 2014, pp. 1413-1424
- Print publication:
- August 2014
-
- Article
- Export citation
Absolutely isolated singularities of a differential equation
-
- Journal:
- Compositio Mathematica / Volume 106 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 04 December 2007, pp. 235-246
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation