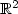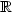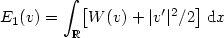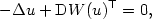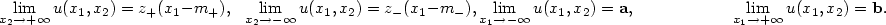In this paper we consider a new kind of Mumford–Shah functionalE(u, Ω) for mapsu : ℝm → ℝnwith m ≥ n. The most important novelty is that theenergy features a singular set Su ofcodimension greater than one, defined through the theory of distributional jacobians.After recalling the basic definitions and some well established results, we prove anapproximation property for the energy E(u, Ω) viaΓ −convergence, in the same spirit of the work by Ambrosio andTortorelli [L. Ambrosio and V.M. Tortorelli, Commun. Pure Appl. Math.43 (1990) 999–1036].

We study the radial-hedgehog solution in a three-dimensional spherical droplet, with homeotropic boundary conditions, within the Landau–de Gennes theory for nematic liquid crystals. The radial-hedgehog solution is a candidate for a global Landau–de Gennes minimiser in this model framework and is also a prototype configuration for studying isolated point defects in condensed matter physics. The static properties of the radial-hedgehog solution are governed by a non-linear singular ordinary differential equation. We study the analogies between Ginzburg–Landau vortices and the radial-hedgehog solution and demonstrate a Ginzburg–Landau limit for the Landau–de Gennes theory. We prove that the radial-hedgehog solution is not the global Landau–de Gennes minimiser for droplets of finite radius and sufficiently low temperatures and prove the stability of the radial-hedgehog solution in other parameter regimes. These results contain quantitative information about the effect of geometry and temperature on the properties of the radial-hedgehog solution and the associated biaxial instabilities.

Let W be a non-negative function of class C3 from $\xR^2$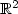 to $\xR$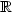, which vanishes exactly at two points a and b. Let S1(a, b) be the set of functions of a real variable which tend to a at -∞ and to b at +∞ and whose one dimensional energy $$ E_1(v)=\int_\xR\bigl[W(v)+\lvert v'\rvert^2/2\bigr]\,\xdif x $$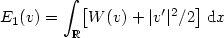 is finite. Assume that there exist two isolated minimizers z+ and z- of the energy E1 over S1(a, b). Under a mild coercivity condition on the potential W and a generic spectral condition on the linearization of the one-dimensional Euler–Lagrange operator at z+ and z-, it is possible to prove that there exists a function u from $\xR^2$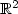 to itself which satisfies the equation $$ -\Delta u + \xDif W(u)^\mathsf{T}=0, $$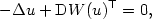 and the boundary conditions $$ \lim_{x_2\to +\infty} u(x_1,x_2)=z_+(x_1-m_+),\phantom{\mathbf{a}} \lim_{x_2\to -\infty} u(x_1,x_2)=z_-(x_1-m_-), \lim_{x_1\to -\infty}u(x_1,x_2)=\mathbf{a},\phantom{z_+(x_1-m_+)} \lim_{x_1\to+\infty}u(x_1,x_2)=\mathbf{b}. $$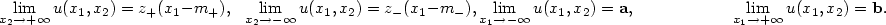 The above convergences are exponentially fast; the numbers m+ and m- are unknowns of the problem.

We consider complex-valued solutions uE of the Ginzburg–Landau equation on a smooth bounded simply connected domain Ω of $\mathbb{R}^N$ , N ≥ 2, where ε > 0 is a small parameter. We assume that the Ginzburg–Landau energy $E_\varepsilon(u_\varepsilon)$ verifies the bound (natural in the context) $E_\varepsilon(u_\varepsilon)\le M_0|\log\varepsilon|$ , where M 0 is some given constant. We also make several assumptions on the boundary data. An important step in the asymptotic analysis of uE, as ε → 0, is to establish uniform Lp bounds for the gradient, for some p>1. We review some recent techniques developed in the elliptic case in [7], discuss some variants, and extend the methods to the associated parabolic equation.