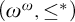1 results
STRUCTURE OF SUMMABLE TALL IDEALS UNDER KATĚTOV ORDER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1-27
-
- Article
- Export citation