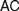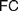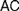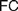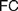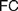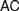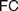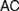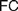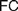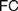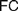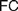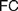Recent discussions on Fregean and neo-Fregean foundations for arithmetic and real analysis pay much attention to what is called either ‘Application Constraint’ (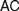 $AC$) or ‘Frege Constraint’ (
$AC$) or ‘Frege Constraint’ (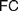 $FC$), the requirement that a mathematical theory be so outlined that it immediately allows explaining for its applicability. We distinguish between two constraints, which we, respectively, denote by the latter of these two names, by showing how
$FC$), the requirement that a mathematical theory be so outlined that it immediately allows explaining for its applicability. We distinguish between two constraints, which we, respectively, denote by the latter of these two names, by showing how 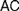 $AC$ generalizes Frege’s views while
$AC$ generalizes Frege’s views while 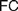 $FC$ comes closer to his original conceptions. Different authors diverge on the interpretation of
$FC$ comes closer to his original conceptions. Different authors diverge on the interpretation of 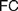 $FC$ and on whether it applies to definitions of both natural and real numbers. Our aim is to trace the origins of
$FC$ and on whether it applies to definitions of both natural and real numbers. Our aim is to trace the origins of 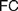 $FC$ and to explore how different understandings of it can be faithful to Frege’s views about such definitions and to his foundational program. After rehearsing the essential elements of the relevant debate (§1), we appropriately distinguish
$FC$ and to explore how different understandings of it can be faithful to Frege’s views about such definitions and to his foundational program. After rehearsing the essential elements of the relevant debate (§1), we appropriately distinguish 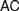 $AC$ from
$AC$ from 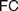 $FC$ (§2). We discuss six rationales which may motivate the adoption of different instances of
$FC$ (§2). We discuss six rationales which may motivate the adoption of different instances of 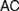 $AC$ and
$AC$ and 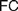 $FC$ (§3). We turn to the possible interpretations of
$FC$ (§3). We turn to the possible interpretations of 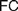 $FC$ (§4), and advance a Semantic
$FC$ (§4), and advance a Semantic 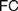 $FC$ (§4.1), arguing that while it suits Frege’s definition of natural numbers (4.1.1), it cannot reasonably be imposed on definitions of real numbers (§4.1.2), for reasons only partly similar to those offered by Crispin Wright (§4.1.3). We then rehearse a recent exchange between Bob Hale and Vadim Batitzky to shed light on Frege’s conception of real numbers and magnitudes (§4.2). We argue that an Architectonic version of
$FC$ (§4.1), arguing that while it suits Frege’s definition of natural numbers (4.1.1), it cannot reasonably be imposed on definitions of real numbers (§4.1.2), for reasons only partly similar to those offered by Crispin Wright (§4.1.3). We then rehearse a recent exchange between Bob Hale and Vadim Batitzky to shed light on Frege’s conception of real numbers and magnitudes (§4.2). We argue that an Architectonic version of 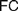 $FC$ is indeed faithful to Frege’s definition of real numbers, and compatible with his views on natural ones. Finally, we consider how attributing different instances of
$FC$ is indeed faithful to Frege’s definition of real numbers, and compatible with his views on natural ones. Finally, we consider how attributing different instances of 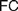 $FC$ to Frege and appreciating the role of the Architectonic
$FC$ to Frege and appreciating the role of the Architectonic 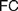 $FC$ can provide a more perspicuous understanding of his foundational program, by questioning common pictures of his logicism (§5).
$FC$ can provide a more perspicuous understanding of his foundational program, by questioning common pictures of his logicism (§5).