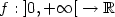We investigate the small deviations under various norms for stable processes defined by the convolution of a smooth function $f : \; ]0, +\infty[ \;\to \mathbb{R}$ 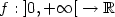with a real SαS Lévy process. We show that the small ball exponent is uniquely determined by the norm and by the behaviour of f at zero, which extends the results of Lifshits and Simon, Ann. Inst. H. Poincaré Probab. Statist.41 (2005) 725–752where this was proved for f being a power function (Riemann-Liouville processes). In the Gaussian case, the same generality as Lifshits and Simon, Ann. Inst. H. Poincaré Probab. Statist.41 (2005) 725–752 is obtained with respect to the norms, thanks to a weak decorrelation inequality due to Li, Elec. Comm. Probab.4 (1999) 111–118. In the more difficult non-Gaussian case, we use a different method relying on comparison of entropy numbers and restrict ourselves to Hölder and L p -norms.

We investigate the asymptotic behaviour of the entropy numbers of the compact embedding $B^{s_1}_{p_1,q_1}(\mathbb{R}^d,w_1)\hookrightarrow B^{s_2}_{p_2,q_2}(\mathbb{R}^d,w_2)$. Here $B^s_{p,q}(\mathbb{R}^d,w)$ denotes a weighted Besov space. We present a general approach which allows us to work with a large class of weights.