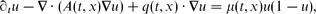The problem of distributing two conducting materials with a prescribed volume ratio in aball so as to minimize the first eigenvalue of an elliptic operator with Dirichletconditions is considered in two and three dimensions. The gap ε between the twoconductivities is assumed to be small (low contrast regime). The main result of the paperis to show, using asymptotic expansions with respect to ε and to small geometricperturbations of the optimal shape, that the global minimum of the first eigenvalue in lowcontrast regime is either a centered ball or the union of a centered ball and of acentered ring touching the boundary, depending on the prescribed volume ratio between thetwo materials.

We investigate in this paper the dependence relation between the space–time periodic coefficients A, q and μ of the reaction–diffusion equation 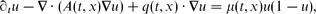and the spreading speed of the solutions of the Cauchy problem associated with compactly supported initial data. We prove in particular that (1) taking the spatial or temporal average of μ decreases the minimal speed, (2) if μ is not constant with respect to x, then increasing the amplitude of the diffusion matrix A does not necessarily increase the minimal speed and (3) if A = IN, μ is a constant, then the introduction of a space periodic drift term q = ∇Q decreases the minimal speed. In order to prove these results, we use a variational characterisation of the spreading speed that involves a family of periodic principal eigenvalues associated with the linearisation of the equation near zero. We are thus back to the investigation of the dependence relation between this family of eigenvalues and the coefficients.