3 results
8 - Real Analysis
- from Part III - Where Are the Paradoxes?
-
- Book:
- Paradoxes and Inconsistent Mathematics
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 230-255
-
- Chapter
- Export citation
ON THE NUMBER OF DEDEKIND CUTS AND TWO-CARDINAL MODELS OF DEPENDENT THEORIES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 23 January 2015, pp. 771-784
- Print publication:
- October 2016
-
- Article
- Export citation
Heirs of box types in polynomially bounded structures
-
- Journal:
- The Journal of Symbolic Logic / Volume 74 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1225-1263
- Print publication:
- December 2009
-
- Article
- Export citation


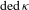

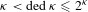

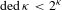

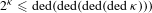
 of
of 