A prominent problem in knowledge representation is how to answer queries taking into account also the implicit consequences of an ontology representing domain knowledge. While this problem has been widely studied within the realm of description logic ontologies, it has been surprisingly neglected within the context of vague or imprecise knowledge, particularly from the point of view of mathematical fuzzy logic. In this paper, we study the problem of answering conjunctive queries and threshold queries w.r.t. ontologies in fuzzy DL-Lite. Specifically, we show through a rewriting approach that threshold query answering w.r.t. consistent ontologies remains in 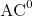${AC}^{0}$ in data complexity, but that conjunctive query answering is highly dependent on the selected triangular norm, which has an impact on the underlying semantics. For the idempotent Gödel t-norm, we provide an effective method based on a reduction to the classical case.