1 results
The abscissa of convergence of the Laplace transform
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 353-362
- Print publication:
- June 1992
-
- Article
- Export citation

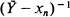 where
where 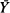 is the mean of the sample values overshooting
is the mean of the sample values overshooting 