11 results
Optimal Buy/Sell Rules for Correlated Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 33-44
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
A Diffusion Limit for Generalized Correlated Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 60-73
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Gillis' Random Walks on Graphs
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 295-301
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Stopping the maximum of a correlated random walk, with cost for observation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 998-1007
- Print publication:
- December 2004
-
- Article
- Export citation
Optimal stopping rules for correlated random walks with a discount
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 483-496
- Print publication:
- June 2004
-
- Article
- Export citation
Optimal stopping rules for directionally reinforced processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 483-504
- Print publication:
- June 2001
-
- Article
- Export citation
The correlated random walk with boundaries: A combinatorial solution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 470-479
- Print publication:
- June 2000
-
- Article
- Export citation
Some Problems on a One-Dimensional Correlated Random Walk with Various Types of Barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 196-201
- Print publication:
- March 1992
-
- Article
- Export citation
The high-order autocovariance structure of the telegraph wave
-
- Journal:
- Journal of Applied Probability / Volume 25 / Issue 4 / December 1988
- Published online by Cambridge University Press:
- 14 July 2016, pp. 744-751
- Print publication:
- December 1988
-
- Article
- Export citation
The discrete uhlenbeck–ornstein process
-
- Journal:
- Journal of Applied Probability / Volume 24 / Issue 4 / December 1987
- Published online by Cambridge University Press:
- 14 July 2016, pp. 908-917
- Print publication:
- December 1987
-
- Article
- Export citation
The correlated random walk
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 2 / June 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 403-414
- Print publication:
- June 1981
-
- Article
- Export citation

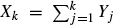 such that (
such that (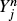 takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the
takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the 