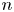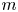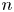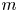A company with $n$ geographically widely dispersed sites seeks insurance that pays off if $m$ out of the $n$ sites experience rarely occurring catastrophes (e.g., earthquakes) during a year. This study describes an adaptive dynamic strategy that enables an insurance company to offer the policy with smaller loss probability than more conventional static policies induce, but at a comparable or lower premium. The strategy accomplishes this by periodically purchasing reinsurance on individual sites. Exploiting rarity, the policy induces zero loss with probability one if no more than one quake occurs during any review interval. The policy also may induce a profit if $m$ or more quakes occur in an interval if no quakes have occurred in previous intervals. The study also examines the benefit of more than one reinsurance policy per active site. The study relies on expected utility to determine indifference premiums and derives an upper bound on loss probability independent of premium.

This paper focuses on the distribution of Poisson sums of discounted claims over a finite or infinite time period. It gives two new results when claim amounts follow Mittag-Leffler distributions and two new results when claim amounts follow gamma distributions. Further, as Mittag-Leffler distribution is of heavy-tailed nature and its moments only exist for order strictly smaller than one, this distribution can be used for modelling insurance whose claim amounts are extremely large, that is, catastrophe insurance.