Jobs arrive at a buffer from which there are several parallel routes to a destination. A socially optimal policy is one which minimizes the average delay of all jobs, whereas an individually optimal policy is one which, for each job, minimizes its own delay, with route preference given to jobs at the head of the buffer. If there is a socially optimal policy for a system with no arrivals, which can be implemented by each job following a policy γ in such a way that no job ever utilizes a previously declined route, then we show that such a γ is an individually optimal policy for each job. Moreover γ continues to be individually optimal even if the system has an arbitrary arrival process, subject only to the restriction that past arrivals are independent of future route-traversal times. Thus, γ is an individually optimal policy which is insensitive to the nature of the arrival process. In the particular case where the times to traverse the routes are exponentially distributed with a possibly different mean time for each of the parallel routes, then such an insensitive individually optimal policy does in fact exist and is moreover trivially determined by certain threshold numbers. A conjecture is also made about more general situations where such individually optimal policies exist.

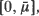 , where cost
, where cost 