1 results
Limiting diffusion for random walks with drift conditioned to stay positive
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 2 / June 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 280-291
- Print publication:
- June 1978
-
- Article
- Export citation
-
Let {ξk : k ≧ 1} be a sequence of independent, identically distributed random variables with E{ξ1} = μ ≠ 0. Form the random walk {Sn : n ≧ 0} by setting S0, Sn = ξ1 + ξ2 + ··· + ξn, n ≧ 1. Define the random function Xn by setting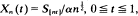
where α is a norming constant. Let N denote the hitting time of the set (–∞, 0] by the random walk. The principal result in this paper is to show (under appropriate conditions on the distribution of ξ1) that the finite-dimensional distributions of Xn, conditioned on n < N < ∞ converge to those of the Brownian excursion process.
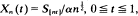where 