1 results
Optimality of myopic stopping times for geometric discounting
-
- Journal:
- Journal of Applied Probability / Volume 25 / Issue 2 / June 1988
- Published online by Cambridge University Press:
- 14 July 2016, pp. 437-443
- Print publication:
- June 1988
-
- Article
- Export citation
-
Consider a sequence of conditionally independent Bernoulli random variables taking on the values 1 and − 1. The objective is to stop the sequence in order to maximize the discounted sum. Suppose the Bernoulli parameter has a beta distribution with integral parameters. It is optimal to stop when the conditional expectation of the next random variable is negative provided the discount factor is less than or equal to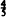
. Moreover, 
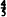is best possible. The case where the parameters of the beta distribution are arbitrary positive numbers is also treated.
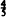. Moreover, 
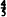is best possible. The case where the parameters of the beta distribution are arbitrary positive numbers is also treated.