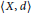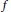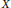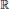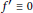This paper constitutes a comprehensive study of ten classes of self-maps on metric spaces 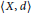 $\langle X\,,\,d\rangle $ with the pointwise (i.e., local radial) and local contraction properties. Each of these classes appeared previously in the literature in the context of fixed point theorems.
$\langle X\,,\,d\rangle $ with the pointwise (i.e., local radial) and local contraction properties. Each of these classes appeared previously in the literature in the context of fixed point theorems.
We begin with an overview of these fixed point results, including concise self contained sketches of their proofs. Then we proceed with a discussion of the relations among the ten classes of self-maps with domains 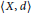 $\langle X\,,\,d\rangle $ having various topological properties that often appear in the theory of fixed point theorems: completeness, compactness, (path) connectedness, rectifiable-path connectedness, and
$\langle X\,,\,d\rangle $ having various topological properties that often appear in the theory of fixed point theorems: completeness, compactness, (path) connectedness, rectifiable-path connectedness, and  $d$-convexity. The bulk of the results presented in this part consists of examples of maps that show non-reversibility of the previously established inclusions between these classes. Among these examples, the most striking is a differentiable auto-homeomorphism
$d$-convexity. The bulk of the results presented in this part consists of examples of maps that show non-reversibility of the previously established inclusions between these classes. Among these examples, the most striking is a differentiable auto-homeomorphism 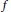 $f$ of a compact perfect subset
$f$ of a compact perfect subset 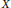 $X$ of
$X$ of 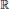 $\mathbb{R}$ with
$\mathbb{R}$ with 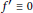 ${{f}^{'}}\,\equiv \,0$, which constitutes also a minimal dynamical system. We finish by discussing a few remaining open problems on whether the maps with specific pointwise contraction properties must have the fixed points.
${{f}^{'}}\,\equiv \,0$, which constitutes also a minimal dynamical system. We finish by discussing a few remaining open problems on whether the maps with specific pointwise contraction properties must have the fixed points.