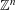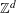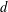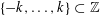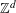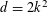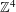3 results
TILING WITH PUNCTURED INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 181-189
- Print publication:
- 2019
-
- Article
- Export citation
ON A STRONG VERSION OF THE KEPLER CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 August 2012, pp. 23-30
- Print publication:
- January 2013
-
- Article
-
- You have access
- Export citation
NATURAL TILING, LATTICE TILING AND LEBESGUE MEASURE OF INTEGRAL SELF-AFFINE TILES
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 18 August 2006, pp. 184-204
- Print publication:
- August 2006
-
- Article
- Export citation