3 results
Best Simultaneous approximation of quasi-continuous functions by monotone functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-408
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
On the error estimates for the Rayleigh-Schrödinger series and the Kato-Rellich perturbation series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 456-468
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
An N-Parameter Chebyshev Set which is not a Sun
-
- Journal:
- Canadian Mathematical Bulletin / Volume 18 / Issue 4 / October 1975
- Published online by Cambridge University Press:
- 20 November 2018, pp. 489-492
- Print publication:
- October 1975
-
- Article
-
- You have access
- Export citation

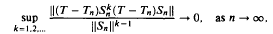
 containing an isolated point.
containing an isolated point.