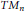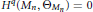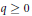3 results
EXTENSION OF COHOMOLOGY CLASSES FOR VECTOR BUNDLES WITH SINGULAR HERMITIAN METRICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-19
-
- Article
- Export citation
cohomologie automorphe et compactifications partielles de certaines variétés de griffiths–schmid
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 5 / September 2005
- Published online by Cambridge University Press:
- 01 September 2005, pp. 1081-1102
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
On Deformations of the Complex Structure on the Moduli Space of Spatial Polygons
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 3 / 01 September 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-421
- Print publication:
- 01 September 2002
-
- Article
-
- You have access
- Export citation