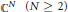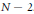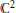4 results
A Radó theorem for complex spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 17 June 2021, pp. 466-472
- Print publication:
- June 2022
-
- Article
- Export citation
Lp-curvature and the Cauchy-Riemann equation near an isolated singular point
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 35-51
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Each Copy of the Real Line in
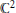 is Removable
is Removable
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 1 / 01 March 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 126-128
- Print publication:
- 01 March 2001
-
- Article
-
- You have access
- Export citation
Continuation of Complex Varieties Across Rectifiable Sets
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 4 / 01 August 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 877-896
- Print publication:
- 01 August 1995
-
- Article
-
- You have access
- Export citation

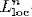 -curvature, to admit the Sobolev inequality and to have suitable volume growth near
-curvature, to admit the Sobolev inequality and to have suitable volume growth near 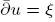 has a smooth solution on a punctured neighbourhood of
has a smooth solution on a punctured neighbourhood of  is Removable
is Removable