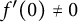4 results
Improved Bloch and Landau constants for meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1269-1273
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterizations of Morrey type spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 328-344
- Print publication:
- June 2022
-
- Article
- Export citation
Extreme Pick-Nevanlinna Interpolants
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 5 / 01 October 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 977-995
- Print publication:
- 01 October 1999
-
- Article
-
- You have access
- Export citation
Weighted Polynomial Approximation of Entire Functions on Unbounded Subsets of the Complex Plane
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 3 / 01 September 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-313
- Print publication:
- 01 September 1993
-
- Article
-
- You have access
- Export citation