Let F be a non-archimedean locally compact field of residual characteristic p, let 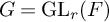$G=\operatorname {GL}_{r}(F)$ and let 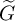$\widetilde {G}$ be an n-fold metaplectic cover of G with 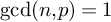$\operatorname {gcd}(n,p)=1$. We study the category 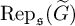$\operatorname {Rep}_{\mathfrak {s}}(\widetilde {G})$ of complex smooth representations of 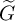$\widetilde {G}$ having inertial equivalence class 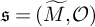$\mathfrak {s}=(\widetilde {M},\mathcal {O})$, which is a block of the category 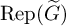$\operatorname {Rep}(\widetilde {G})$, following the ‘type theoretical’ strategy of Bushnell-Kutzko.

Precisely, first we construct a ‘maximal simple type’ 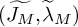$(\widetilde {J_{M}},\widetilde {\lambda }_{M})$ of 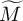$\widetilde {M}$ as an 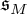$\mathfrak {s}_{M}$-type, where 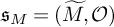$\mathfrak {s}_{M}=(\widetilde {M},\mathcal {O})$ is the related cuspidal inertial equivalence class of 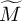$\widetilde {M}$. Along the way, we prove the folklore conjecture that every cuspidal representation of 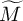$\widetilde {M}$ could be constructed explicitly by a compact induction. Secondly, we construct ‘simple types’ 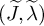$(\widetilde {J},\widetilde {\lambda })$ of 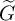$\widetilde {G}$ and prove that each of them is an 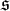$\mathfrak {s}$-type of a certain block 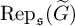$\operatorname {Rep}_{\mathfrak {s}}(\widetilde {G})$. When 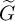$\widetilde {G}$ is either a Kazhdan-Patterson cover or Savin’s cover, the corresponding blocks turn out to be those containing discrete series representations of 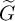$\widetilde {G}$. Finally, for a simple type 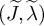$(\widetilde {J},\widetilde {\lambda })$ of 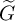$\widetilde {G}$, we describe the related Hecke algebra 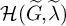$\mathcal {H}(\widetilde {G},\widetilde {\lambda })$, which turns out to be not far from an affine Hecke algebra of type A, and is exactly so if 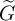$\widetilde {G}$ is one of the two special covers mentioned above.

We leave the construction of a ‘semi-simple type’ related to a general block 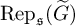$\operatorname {Rep}_{\mathfrak {s}}(\widetilde {G})$ to a future phase of the work.

We prove that either the images of the mapping class groups by quantum representations are not isomorphic to higher rank lattices or else the kernels have a large number of normal generators. Further, we show that the images of the mapping class groups have non-trivial 2-cohomology, at least for small levels. For this purpose, we considered a series of quasi-homomorphisms on mapping class groups extending the previous work of Barge and Ghys (Math. Ann. 294 (1992), 235–265) and of Gambaudo and Ghys (Bull. Soc. Math. France 133(4) (2005), 541–579). These quasi-homomorphisms are pull-backs of the Dupont–Guichardet–Wigner quasi-homomorphisms on pseudo-unitary groups along quantum representations.

The aim of this work is to provide a new approach for constructing $n$-dimensional Steinberg symbols on discrete valuation fields from $\left( n\,+\,1 \right)$-cocycles and to study reciprocity laws on curves related to these symbols.