Let A ≤ B be structures, and ${\cal K}$ a class of structures. An element b ∈ B is dominated by A relative to ${\cal K}$ if for all ${\bf{C}} \in {\cal K}$ and all homomorphisms g, g' : B → C such that g and g' agree on A, we have gb = g'b. Our main theorem states that if ${\cal K}$ is closed under ultraproducts, then A dominates b relative to ${\cal K}$ if and only if there is a partial function F definable by a primitive positive formula in ${\cal K}$ such that FB(a1,…,an) = b for some a1,…,an ∈ A. Applying this result we show that a quasivariety of algebras ${\cal Q}$ with an n-ary near-unanimity term has surjective epimorphisms if and only if $\mathbb{S}\mathbb{P}_n \mathbb{P}_u \left( {\mathcal{Q}_{{\text{RSI}}} } \right)$ has surjective epimorphisms. It follows that if ${\cal F}$ is a finite set of finite algebras with a common near-unanimity term, then it is decidable whether the (quasi)variety generated by ${\cal F}$ has surjective epimorphisms.

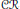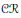In previous papers, Barr and Raphael investigated the situation of a topological space $Y$ and a subspace $X$ such that the induced map $C(Y)\,\to \,C(X)$ is an epimorphism in the category $\mathcal{C}\mathcal{R}$ of commutative rings (with units). We call such an embedding a $\mathcal{C}\mathcal{R}$-epic embedding and we say that $X$ is absolute $\mathcal{C}\mathcal{R}$-epic if every embedding of $X$ is $\mathcal{C}\mathcal{R}$-epic. We continue this investigation. Our most notable result shows that a Lindelöf space $X$ is absolute $\mathcal{C}\mathcal{R}$-epic if a countable intersection of $\beta X$-neighbourhoods of $X$ is a $\beta X$-neighbourhood of $X$. This condition is stable under countable sums, the formation of closed subspaces, cozero-subspaces, and being the domain or codomain of a perfect map. A strengthening of the Lindelöf property leads to a new class with the same closure properties that is also closed under finite products. Moreover, all $\sigma $-compact spaces and all Lindelöf $P$-spaces satisfy this stronger condition. We get some results in the non-Lindelöf case that are sufficient to show that the Dieudonné plank and some closely related spaces are absolute $\mathcal{C}\mathcal{R}$-epic.

We study Tychonoff spaces $X$ with the property that, for all topological embeddings $X\,\to \,Y$, the induced map $C(Y)\,\to \,C(X)$ is an epimorphism of rings. Such spaces are called absolute 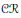$\mathcal{C}\mathcal{R}$-epic. The simplest examples of absolute $\mathcal{C}\mathcal{R}$-epic spaces are $\sigma $-compact locally compact spaces and Lindelöf $P$-spaces. We show that absolute $\mathcal{C}\mathcal{R}$-epic first countable spaces must be locally compact.

However, a “bad” class of absolute $\mathcal{C}\mathcal{R}$-epic spaces is exhibited whose pathology settles, in the negative, a number of open questions. Spaces which are not absolute $\mathcal{C}\mathcal{R}$-epic abound, and some are presented.

In this paper we study categorical compactness with respect to a class of objects F being motiveated by examples arising from modules, abelian groups, and various classes of non-abelian groups. This theory is then applied to the category of not necessarily associative rings. In particular, we study the example arising from the class of all torsion-free rings. This work extends some recent results of B. J. Gardner for associative rings and radical classes.

A total category is constructed which has no regular generator although it has an object C such that every object is a regular quotient of a copower of C.

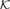
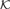
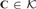
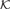
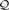
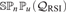
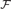
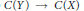
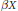
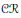
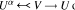Let K be a category of structures with all its homomorphisms, Uα K → Set the α-th power of its forgetful functor U An α-ary implicit partial operation (O.P.I.) in K is a diagram of natural transformations and functors. We first study various properties which O P I's can have, as maximality, definability and closure under products or equalizers. Revisiting various concepts and results of Isbell, Linton, Bacsich and Herrera, we note, among other things, that the dominion (resp. the stable dominion) of a subset of a structure K is its closure under O P I's (resp. under equalizer-closed O P I's), and we show that in a variety, all epis are surjective (resp. all monos are regular) iff all limit-closed (resp. product-closed) O P I's are restrictions of total implicit operations.