Let  $R$ be a ring. A map
$R$ be a ring. A map 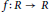 $f\,:\,R\,\to \,R$ is additive if
$f\,:\,R\,\to \,R$ is additive if 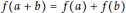 $f(a\,+\,b)\,=\,f(a)\,+\,f(b)$ for all elements
$f(a\,+\,b)\,=\,f(a)\,+\,f(b)$ for all elements  $a$ and
$a$ and  $b$ of
$b$ of  $R$. Here, a map
$R$. Here, a map 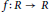 $f\,:\,R\,\to \,R$ is called unit-additive if
$f\,:\,R\,\to \,R$ is called unit-additive if 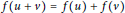 $f(u\,+\,v)\,=\,f(u)\,+\,f(v)$ for all units
$f(u\,+\,v)\,=\,f(u)\,+\,f(v)$ for all units  $u$ and
$u$ and  $v$ of
$v$ of  $R$. Motivated by a recent result of
$R$. Motivated by a recent result of 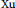 $\text{Xu}$,
$\text{Xu}$, 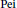 $\text{Pei}$ and
$\text{Pei}$ and 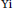 $\text{Yi}$ showing that, for any field
$\text{Yi}$ showing that, for any field  $F$, every unit-additive map of
$F$, every unit-additive map of 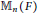 ${{\mathbb{M}}_{n}}(F)$
is additive for all
${{\mathbb{M}}_{n}}(F)$
is additive for all 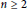 $n\,\ge \,2$, this paper is about the question of when every unit-additivemap of a ring is additive. It is proved that every unit-additivemap of a semilocal ring
$n\,\ge \,2$, this paper is about the question of when every unit-additivemap of a ring is additive. It is proved that every unit-additivemap of a semilocal ring  $R$ is additive if and only if either
$R$ is additive if and only if either  $R$ has no homomorphic image isomorphic to
$R$ has no homomorphic image isomorphic to 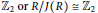 ${{\mathbb{Z}}_{2}}\,\text{or}\,R/J(R)\,\cong \,{{\mathbb{Z}}_{2}}\,$ with
${{\mathbb{Z}}_{2}}\,\text{or}\,R/J(R)\,\cong \,{{\mathbb{Z}}_{2}}\,$ with 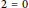 $2\,=\,0$ in
$2\,=\,0$ in  $R$. Consequently, for any semilocal ring
$R$. Consequently, for any semilocal ring  $R$, every unit-additive map of
$R$, every unit-additive map of 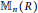 ${{\mathbb{M}}_{n}}(R)$ is additive for all
${{\mathbb{M}}_{n}}(R)$ is additive for all 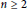 $n\,\ge \,2$. These results are further extended to rings
$n\,\ge \,2$. These results are further extended to rings  $R$ such that
$R$ such that 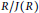 $R/J(R)$ is a direct product of exchange rings with primitive factors Artinian. A unit-additive map
$R/J(R)$ is a direct product of exchange rings with primitive factors Artinian. A unit-additive map 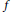 $f$ of a ring
$f$ of a ring  $R$ is called unithomomorphic if
$R$ is called unithomomorphic if 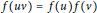 $f(uv)\,=\,f(u)f(v)$ for all units
$f(uv)\,=\,f(u)f(v)$ for all units  $u$,
$u$,  $v$ of
$v$ of  $R$. As an application, the question of when every unit-homomorphic map of a ring is an endomorphism is addressed.
$R$. As an application, the question of when every unit-homomorphic map of a ring is an endomorphism is addressed.