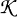Define dx to be the codimension of the top nonvanishing homology group of the manifold X with coefficients in 2. We investigate homogeneous spaces X := G/H, where G is a connected complex Lie group and H is a closed complex subgroup for which dx = 1,2 and O(X) ≠ ℂ. There exists a fibration π: G/H → G/U such that G/U is holomorphically separable and π*(O(G/U)) = O(G/H), see [11]. We prove the following. If dx = 1, then F := U/H is compact and connected and Y :=G/U is an affine cone with its vertex removed. If dx = 2, then either F is connected with dF = 1 and Y is an affine cone with its vertex removed, or F is compact and connected and dy = 2, where Y is ℂ, the affine quadric Q2, ℙ2 — Q (with Q a quadric curve) or a homogeneous holomorphic * -bundle over an affine cone minus its vertex which is itself an algebraic principal bundle or which admits a two-to-one covering that is.

A Lie algebra is called a Heisenberg algebra if its centre coincides with its derived algebra and is one-dimensional. When is infinite-dimensional, Kac, Kazhdan, Lepowsky, and Wilson have proved that -modules that satisfy certain conditions are direct sums of a canonical irreducible submodule. This is an algebraic analogue of the Stone-von Neumann theorem. In this paper, we extract quantum Heisenberg algebras, q(), from the quantum affine algebras whose vertex representations were constructed by Frenkel and Jing. We introduce the canonical irreducible q()-module Mq and a class Cq of q()-modules that are shown to have the Stone-von Neumann property. The only restriction we place on the complex number q is that it is not a square root of 1. If q1 and q2 are not roots of unity, or are both primitive m-th roots of unity, we construct an explicit isomorphism between q1() and q2(). If q1 is a primitive m-th root of unity, m odd, q2 a primitive 2m-th or a primitive 4m-th root of unity, we also construct an explicit isomorphism between q1() and q2().

In this paper, we study the restriction of irreducible representations of the group SO2n+1 × SO2m to a spherical subgroup.

Let A be a finite set with |A| > 2. We describe all clones on A containing the set SA of all permutations of A among its unary operations. (A clone on A is a composition closed set of finitary operations on A containing all projections). With a few exceptions such a clone C is either essentially unary or cellular i.e. there exists a monoid M of self-maps of A containing SA such that either C = (= all essentially unary operations agreeing with some f ∊ M) or C = ∪ Гh where 1 < h ≤ |A| and Гh consists of all finitary operations on A taking at most h values. The exceptions are subclones of Burle's clone or of its variant (provided |A| is even).

A module M is said to be weakly N-projective if it has a projective cover π: P(M) ↠M and for each homomorphism : P(M) → N there exists an epimorphism σ:P(M) ↠M such that 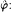(kerσ) = 0, equivalently there exists a homomorphism :M ↠N such that σ= 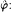. A module M is said to be weakly projective if it is weakly N-projective for all finitely generated modules N. Weakly N-injective and weakly injective modules are defined dually. In this paper we study rings over which every weakly injective right R-module is weakly projective. We also study those rings over which every weakly projective right module is weakly injective. Among other results, we show that for a ring R the following conditions are equivalent:

(1) R is a left perfect and every weakly projective right R-module is weakly injective.

(2) R is a direct sum of matrix rings over local QF-rings.

(3) R is a QF-ring such that for any indecomposable projective right module eR and for any right ideal I, soc(eR/eI) = (eR/eJ)n for some positive integer n.

(4) R is right artinian ring and every weakly injective right R-module is weakly projective.

(5) Every weakly projective right R-module is weakly injective and every weakly injective right R-module is weakly projective.

The summability fields of generalized Nörlund means (N,p*α,p), α ∈ Ν, are increasing with a and are contained in that of the corresponding power series method (P,p). Particular cases are the Cesàro- and Euler-means with corresponding power series methods of Abel and Borel. In this paper we generalize a convexity theorem, which is well-known for the Cesàro means and which was recently shown for the Euler means to a large class of generalized Nörlund means.

In singularity theory, J. Damon gave elegant versions of the unfolding and determinacy theorems for geometric subgroups of . and . In this work, we propose a unified treatment of the smooth stability of germs and the structural stability of versai unfoldings for a large class of such subgroups.

Compact C*-convex subsets of Mn correspond exactly to n-th matrix ranges of operators. The main result of this paper is to discover the “right” analog of linear extreme points, called structural elements, and then to prove a generalised Krein-Milman theorem for C*-convex subsets of Mn. The relationship between structural elements and an earlier attempted generalisation, called C*-extreme points, is examined, solving affirmatively a conjecture of Loebl and Paulsen [8]. An improved bound for a C* -convex version of the Caratheodory theorem for convex sets is also given.

We investigate left conjugacy closed loops which can be given by invariant sections in the group generated by their left translations. These loops are generalizations of the conjugacy closed loops introduced in [13] just as Bol loops generalize Moufang loops. The relations of these loops to common classes of loops are studied. For instance on a connected manifold we construct proper topological left conjugacy closed loops satisfying the left Bol condition but show that any differentiable such loop must be a group. We show that the configurational condition in the 3-net corresponding to an isotopy class of left conjugacy closed loops has the same importance in the geometry of 3-nets as the Reidemeister or the Bol condition.

In this paper we characterize weighted Lorentz norm inequalities for the one sided Hardy-Littlewood maximal function

Similar questions are discussed for the maximal operator associated to an invertible measure preserving transformation of a measure space.

The heat kernel of an amenable Lie group satisfies either exp. We give a condition on the Lie algebra which characterizes the two cases.

We prove that a commutative preordered semigroup embeds into the space of all equidecomposability types of subsets of some set equipped with a group action (in short, a full type space) if and only if it satisfies the following axioms: (i) (⩝x,y) (x ≤ x + y); (ii) (⩝x,y)((x ≤ y and y ≤ x) ⇒ x = y); (iii) (⩝x,y,u, v)((x + u ≤ y + u and u ≤ v) ⩝ x + v ≤ y ≤ v); (iv) (⩝x, u, V)((x + u = u and u ≤ v) ⇒ x + v = v); (v) (⩝x,y)(mx ≤ my ⇒ x ≤ y) (all m ∊ Ν \ {0}). Furthermore, such a structure can always be embedded into a reduced power of the space Τ of nonempty initial segments of + with rational (possibly infinite) endpoints, equipped with the addition defined by and the ordering defined by . As a corollary, the set of all universal formulas of (+, ≤) satisfied by all full type spaces is decidable.