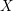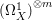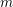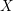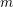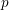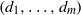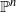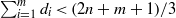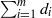3 results
SINGULAR RATIONALLY CONNECTED THREEFOLDS WITH NON-ZERO PLURI-FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 3-32
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
Approximately Rationally or Elliptically Connected Varieties
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 17 December 2013, pp. 281-297
-
- Article
-
- You have access
- Export citation
Spaces of rational curves on complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 March 2013, pp. 1041-1060
- Print publication:
- June 2013
-
- Article
- Export citation