1 results
IP-Sets on the Circle
-
- Journal:
- Canadian Journal of Mathematics / Volume 42 / Issue 4 / 01 August 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 575-589
- Print publication:
- 01 August 1990
-
- Article
-
- You have access
- Export citation

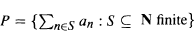 for a certain sequence
for a certain sequence 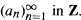 The main questions studied here are : (1) Under what conditions on (
The main questions studied here are : (1) Under what conditions on (