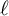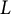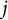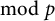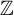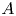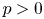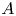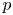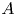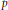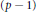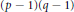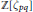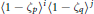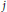5 results
On elements of prescribed norm in maximal orders of a quaternion algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 111-139
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
Reductions of abelian surfaces over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 893-950
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An Extension of Craig's Family of Lattices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 645-653
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
Small Zeros of Quadratic Forms Avoiding a Finite Number of Prescribed Hyperplanes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-65
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation