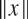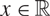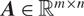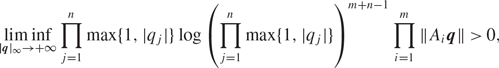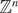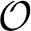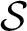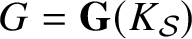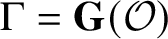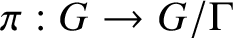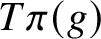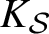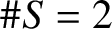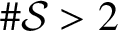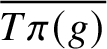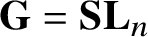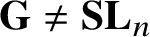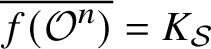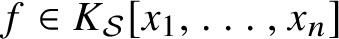3 results
Multiplicatively badly approximable matrices up to logarithmic factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 685-703
- Print publication:
- May 2022
-
- Article
- Export citation
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3142-3177
- Print publication:
- October 2021
-
- Article
- Export citation
Small Zeros of Quadratic Forms Avoiding a Finite Number of Prescribed Hyperplanes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-65
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation