3 results
On the Distribution of the Sequence {nd*(n)}
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 1 / 01 March 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-108
- Print publication:
- 01 March 1989
-
- Article
-
- You have access
- Export citation
Cubic and Higher Order Algorithms for π
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 436-443
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation
Beatty Sequences, Continued Fractions, and Certain Shift Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 19 / Issue 4 / 01 December 1976
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-482
- Print publication:
- 01 December 1976
-
- Article
-
- You have access
- Export citation

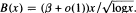 . In this note we give an explicit expression for
. In this note we give an explicit expression for 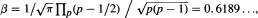 where the product is over all primes
where the product is over all primes 